Zufallszahlen erzeugen

R bringt mehrere Generatoren für Zufallszahlen mit

Zufallszahlen spielen oft eine wichtige Rolle bei der Analyse von Daten. R bringt eine Reihe von Funktionen mit, die solche Zahlen aus verschiedenen Verteilungen generieren.
Genau genommen erzeugt R aber Pseudozufallszahlen, da diese von einem Algorithmus berechnet werden und der Zufall dabei keine Rolle spielt. Doch für die meisten Zwecke sind solche Zufallszahlen gut genug (siehe auch Wikipedia).
Um gleichförmig verteilte Zufallszahlen zu erzeugen bietet R die Funktion runif(). Sie erzeugt standardmäßig Zahlen zwischen 0 und 1. Das Intervall lässt sich aber nach Belieben anpassen. Alternativ kannst du auch die Funktion sample() verwenden.

> runif(1)
[1] 0.5595902
> # generiere einen Vector mit 4 Zufallszahlen
> runif(4)
[1] 0.6563260 0.4757386 0.4896942 0.6060721
> # erzeuge 3 Integer-Zahlen zwischen 0 und 100
> floor(runif(3, min=0, max=101))
[1] 58 51 80
> sample(1:100, 3, replace=TRUE)
[1]  5 12 14

Die Gleichverteiltheit dieser Pseudozufallszahlen lässt sich leicht mit Hilfe eines Histogramms dokumentieren.

r <- runif(1000, min=0, max=100)
hist(r)

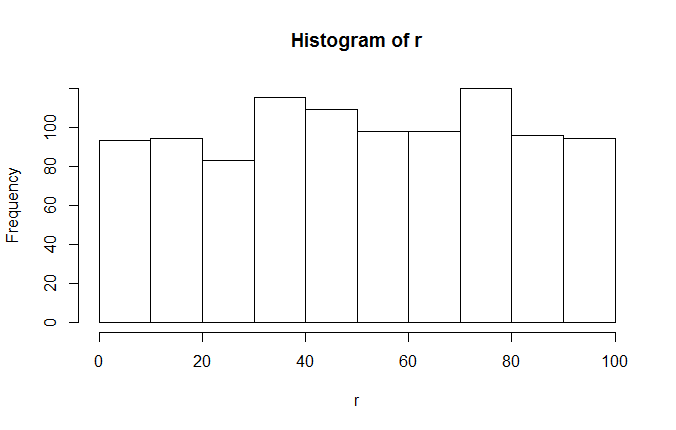
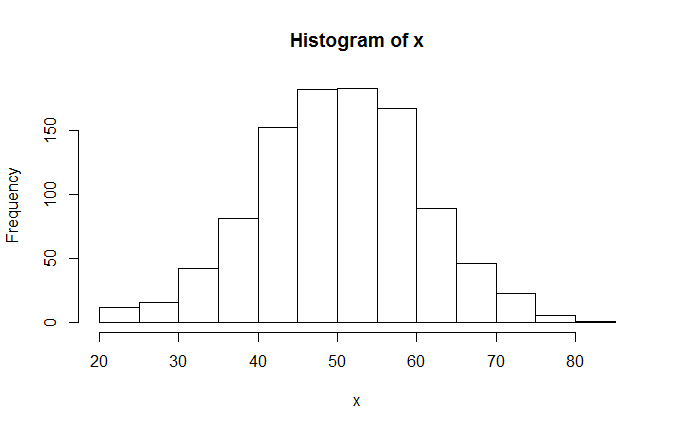
Für manche Zwecke braucht man nicht gleichverteilte, sondern normalverteilte Pseudozufallszahlen. Diese wirft die Funktion rnorm() aus. Als Parameter lässt sich neben der Anzahl der zu erzeugenden Zahlen auch der Mittelwert und die Standardabweichung angeben. Der Unterschied wird im Histogramm deutlich.

x <- rnorm(1000, mean=50, sd=10)
hist(x)

Last but not least gibt es noch reproduzierbare Pseudozufallszahlen. Das klingt zwar paradox, ist aber manchmal sinnvoll, um bestimmte Analysen exakt wiederholen zu können. Dazu erstellst du zunächst einen Seed mit einer beliebigen ganzen Zahl und verwendest dazu die Funktion set.seed().

> set.seed(809)
> runif(3)
[1] 0.08182088 0.11864272 0.22329809
> set.seed(809)
> runif(3)
[1] 0.08182088 0.11864272 0.22329809

Update: Quanten-Zufallszahlen

Anfang 2019 ist das Package qrandom erschienen. Es kann echte Zufallszahlen erzeugen, indem es Quantenfluktiationen des Vakuums nutzt. Der ANU Quantum Random Number Generator wird über eine API-Schnittstelle von der Australian National University zur Verfügung gestellt. Das elektromagnetische Feld des Vakuums weist bei allen Frequenzen zufällige Schwankungen in Phase und Amplitude auf. Durch die sorgfältige Messung dieser Schwankungen lassen sich Zufallszahlen mit hoher Bandbreite erzeugen. Das Package bietet Funktionen zum Abrufen einer Folge von zufälligen ganzen Zahlen oder Hexadezimalen und Stichproben aus einer normalen oder gleichen Verteilung.

## 10 echte Zufallszahlen im Intervall [0; 255]
> library(qrandom)
> randomNumbers <- qrandom(n = 10)
> randomNumbers
 [1] 196  64  17 205  27 195 156  98 204  81
## 10 echte Zufallszahlen im Intervall [0; 65,535]
> randomNumbers <- qrandom(n = 10, type = "uint16")
> randomNumbers
 [1] 27755 21276  6448 18077 24833 22428  7229  6894 52370  8509
## 10 echte hexadezimale Zufallszahlen im Intervall [00; ff]
> randomNumbers <- qrandom(n = 10, type = "hex16")
> randomNumbers
 [1] "4f" "c5" "b5" "99" "11" "17" "12" "6e" "d9" "84"
## 'hex16' sind vom Typ characters
## qrandommaxint()
> randomIntegers <- qrandommaxint(n = 10)
> randomIntegers
 [1]   318785311 -2054761310  -159436187   284469799   992974627  -403647514  2024387444 -1421021840  1360259280
[10]  1126686637
## qRandomSeq ist eine Liste mit 1.000 echten Zufallszahlen für jeden der Datentypen
> data(qRandomSeq)
> View(qRandomSeq)
> qRandomSeq$uint8
[1] 109  82 181  19  61  72 130 170  70 104  95 117 236 249 127 193 210 102   3 235 191 193 187  12 192 236 119 164  66
  [30]  15  42 154 144 189  21 130  56 237 216  85 136 228  76  41 212 248 220 132 123 186  42 214   3 193 194 171 246 217
  [59] 125 191 139  30 168 218   1  96 191 229 105  24  86 229  92  80 166 107 114 107  46 150 237 246  61  12 132 228 175
  [88]  28  54 174 173 187  95 132 186  65  30  27 242   8 221 119  86  85 211 217  87 141  41  23 158   4 237 228  34 115
 [117]  43  80  56 117 219  46 108  57 240 179 155 143  47  79  41 127 174  28 117  12  81 122 192 177 110 171  30 161   0
 [146]  23  34 240 186 221  24 237 166  39 234 189  80  92 225 127 183 149 201 108 247  11 170 197 154  53 126 230 238 181
 [175] 164  24 200  98  14  28 120 132 126 242 206 203 235 208  91 120 114  20 185  77  30 217 106 243 185 211 221  64  96
 [204]  43  84  11 103 255 156 248 132 161 104 236 222 146  19  59  34  36 184 236   9 169  43  59 197 253 120 127 226 121
 [233] 104 152 104 198 157 124 238  99  37  56  37  61 211 156  73 164 112  23 127  49 185 225  64  81 137  83 187 145 100
 [262] 116 123  34 193 134 214  52 212  65 229 130 135 116 161 114 135 199 198 226  35 211 130   5 102 230  90 213 202  90
 [291]  35 105  90 163  84 137  44   0  66  57 181 153 135 138 248  74 112 147 182 255 183 127 139  40 118  61  55  63  67
 [320] 204 171 233 193  11 232 241 108  13 222 106   5  69  38 136 163 158  57  37  21 250 153 223 172  77 115  68  72 129
 [349] 204 240 172  56  84  83 119  48 200 249  83 114 163 227 245 144 147 225 161 174 217  26 203 224 137 114  40 227 250
 [378] 104 228 125 213 158  58 251 236  54  66  47  44 118 181  39 112   1  65 100  59 220 244 101 237 204 111 255 178 185
 [407] 181  59 125 190  21 140  84 116  21  94  61 204 253 144 106 146  84 230 224 243  41 119  78 239 118 107 255  89 228
 [436] 191  23 142 204   8 218 138 154 106  38  30 181  67 243  78  70 164 247 238   9 195  58  91 250  59  12 225   5 218
 [465] 227  25 159  26  14  80 223 103  36  98 135  33 135 153 250  83 226  43 147  37  60 157  26  23  44 145 252 216 173
 [494] 108 206  88  83  40  52  50 131 121 194 115 246  86  92 255 213 154  23  79  31  95 185 162 200 149 218 118  78 110
 [523] 149  74 229 135 126  64  37  48 206 202 160 123 187 114   9  73 199  66 161 203  44 109 237 155 149  41 169 216 179
 [552]  94 237  52 122 224   2 130  82 181 114 216 165 180  60 118 219  78 117   0 232 210  96 219 173 143  15 105 182 200
 [581]  18 236 147 138  48 153 249 129 244 182  89 217 211  46  91 227  14 152 221  44   9 184 219 158 187 101  98 124 223
 [610]  99 214 189 198 174 227 242 236 238 233 135  97 160 167 108  97 154 132 142 168 131  61 163 133 241 209  51 110 224
 [639]  82 205  14 242 176 101   2 230 159 227 188 138 230  82 156 251 228 168 231  31  42  59 101  11   3 226  37 242  16
 [668]  86 111 161 198  18  74 227 167 157  99 154 102 160  39  28 244 255 115  94   5   0  97 208 196 165 103  96  60 170
 [697] 168 121  77   7 177  22 228 163 117 114  64 229  84 120  72 199 154 228  22 196  16 189 138  69 234  35   7 204  74
 [726] 217 208  93 241 107  67  87 109  81 185 101 218  95  16  20 206  31   7 210   5 222 217 239 220  26 232 194 221  66
 [755]   2 134  99 246  99 221 149 210 110  86 230 122 116 134 137   4 204  98 139 245 246 182 212 209  30 194 241 172  80
 [784]  75  20  45  89 241 139 213 129 121 180 251  28  96 152 144 158 230 204 121 125  44 154  29 183   7  91 107 110  89
 [813]  71 239 186  73  75  91 249  33 171  18 168 202 182 120 172  19   5 208 186 110 225 221 252 209 192 164 146 124 238
 [842] 194 212  25 254  65  80 219 110 115  26 123 121  83  79  66 135 156 215 165 215 208  64  41 196 235 245  67   0 108
 [871]  97  45 220 218  26 168 246 125  44 244  62 169 231 154 192 167  15  18 149 138 158 178 175 133  28 123 132 247 115
 [900] 223 214 101 159 187 102 243 132 149 195  84  65  93  12  19  69 194 167 228  71 203 196 234 245 198 186 240 165 170
 [929] 169  40  84 156  42   5  12 167  48  18 224 150 142 165 235 156 236 103 225  25 140 160 235 192  80 112 104   8 247
 [958] 217 182  29 156 127 106  35 197   8  75 140  70   9 227  94 226  94 114 192 125 234  13  86 199  32 202  77 132   8
 [987]  86  23  10 229 115 157 178 122 197 247  36 125 166 200
## um einen Würfel zu simulieren, bedient man sich des Modulo-Operators
> qRandomSeq$uint8 %% 6 + 1
   [1] 2 5 2 2 2 1 5 3 5 3 6 4 3 4 2 2 1 1 4 2 6 2 2 1 1 3 6 3 1 4 1 5 1 4 4 5 3 4 1 2 5 1 5 6 3 3 5 1 4 1 1 5 4 2 3 4 1 2
  [59] 6 6 2 1 1 3 2 1 6 2 4 1 3 2 3 3 5 6 1 6 5 1 4 1 2 1 1 1 2 5 1 1 6 2 6 1 1 6 1 4 3 3 6 6 3 2 2 2 4 4 6 6 3 5 4 1 5 2
 [117] 2 3 3 4 4 5 1 4 1 6 6 6 6 2 6 2 1 5 4 1 4 3 1 4 3 4 1 6 1 6 5 1 1 6 1 4 5 4 1 4 3 3 4 2 4 6 4 1 2 6 3 6 5 6 1 3 5 2
 [175] 3 1 3 3 3 5 1 1 1 3 3 6 2 5 2 1 1 3 6 6 1 2 5 4 6 2 6 5 1 2 1 6 2 4 1 3 1 6 3 3 1 3 2 6 5 1 5 3 4 2 2 6 6 2 1 2 5 2
 [233] 3 3 3 1 2 5 5 4 2 3 2 2 2 1 2 3 5 6 2 2 6 4 5 4 6 6 2 2 5 3 4 5 2 3 5 5 3 6 2 5 4 3 6 1 4 2 1 5 6 2 5 6 1 3 1 4 5 1
 [291] 6 4 1 2 1 6 3 1 1 4 2 4 4 1 3 3 5 4 3 4 4 2 2 5 5 2 2 4 2 1 4 6 2 6 5 2 1 2 1 5 6 4 3 5 2 3 4 2 4 5 4 2 5 6 2 3 1 4
 [349] 1 1 5 3 1 6 6 1 3 4 6 1 2 6 6 1 4 4 6 1 2 3 6 3 6 1 5 6 5 3 1 6 4 3 5 6 3 1 1 6 3 5 2 4 5 2 6 5 6 5 5 6 4 1 4 4 5 6
 [407] 2 6 6 5 4 3 1 3 4 5 2 1 2 1 5 3 1 3 3 4 6 6 1 6 5 6 4 6 1 6 6 5 1 3 3 1 5 5 3 1 2 2 4 1 5 3 2 5 4 4 5 2 5 6 1 4 6 3
 [465] 6 2 4 3 3 3 2 2 1 3 4 4 4 4 5 6 5 2 4 2 1 2 3 6 3 2 1 1 6 1 3 5 6 5 5 3 6 2 3 2 1 3 3 4 4 5 6 2 2 6 6 1 3 6 3 5 1 3
 [523] 6 3 2 4 1 5 2 1 3 5 5 4 2 1 4 2 2 1 6 6 3 2 4 6 6 6 2 1 6 5 4 5 3 3 3 5 5 2 1 1 4 1 1 5 4 1 4 1 5 1 1 4 6 6 4 4 3 3
 [581] 1 3 4 1 1 4 4 4 5 3 6 2 2 5 2 6 3 3 6 3 4 5 4 3 2 6 3 5 2 4 5 4 1 1 6 3 3 5 6 4 2 5 6 1 2 5 1 5 1 6 2 2 2 2 6 4 3 3
 [639] 5 2 3 3 3 6 3 3 4 6 3 1 3 5 1 6 1 1 4 2 1 6 6 6 4 5 2 3 5 3 4 6 1 1 3 6 6 2 4 5 1 5 4 5 5 4 2 5 6 1 2 5 5 4 2 1 1 3
 [697] 1 2 6 2 4 5 1 2 4 1 5 2 1 1 1 2 5 1 5 5 5 4 1 4 1 6 2 1 3 2 5 4 2 6 2 4 2 4 6 6 3 6 5 3 3 2 2 1 6 1 2 6 5 3 5 3 6 1
 [755] 3 3 4 1 4 6 6 1 3 3 3 3 3 3 6 5 1 3 2 6 1 3 3 6 1 3 2 5 3 4 3 4 6 2 2 4 4 2 1 6 5 1 3 1 3 3 1 2 6 3 5 6 4 2 2 6 3 6
 [813] 6 6 1 2 4 2 4 4 4 1 1 5 3 1 5 2 6 5 1 3 4 6 1 6 1 3 3 5 5 3 3 2 3 6 3 4 3 2 3 4 2 6 2 1 4 1 6 4 6 5 5 6 5 2 6 2 1 1
 [871] 2 4 5 3 3 1 1 6 3 5 3 2 4 5 1 6 4 1 6 1 3 5 2 2 5 4 1 2 2 2 5 6 4 2 1 4 1 6 4 1 6 4 1 2 4 3 6 1 6 6 5 1 6 1 1 1 4 3
 [929] 2 5 1 1 1 6 1 6 1 1 3 1 5 4 2 1 3 2 4 2 3 5 2 1 3 5 3 3 2 2 3 6 1 2 5 6 6 3 4 3 5 4 6 5 5 5 1 1 6 1 2 3 2 3 5 6 1 3
 [987] 3 6 5 2 2 2 5 3 6 2 1 6 5 3

Schreiben macht durstig! Spendier mir doch ein Bier, indem du mir einen kleinen Betrag via Paypal schickst oder ein paar Bitcoin- oder Ethereum-Bruchteile an die entsprechende nachfolgende Adresse. Prost & auf dein Wohl!

Bitcoin-Adresse : 1PjYNNjHmkAUmf626hukL32Vs1wFt8v1wT
Ethereum-Adresse : 0x974e73994c7483eef1396a21b9937aecb7b6c286